Chapter 2: Understanding Bayesian Priors in Economic Analysis

In Bayesian analysis, the PRIOR is a probability distribution that represents our knowledge or beliefs about a parameter before we observe any data. It's essentially our initial guess or assumption about the parameter's value.

Detailed Explanation

Definition: The prior distribution, denoted as P(θ), is the probability distribution of the parameter θ before considering the current data. It reflects what we know about θ based on previous information, expert opinion, or historical data.
Example: Suppose we want to estimate the probability of a coin landing heads. Before flipping the coin, we might believe that the coin is fair, so our prior distribution for the probability of heads (θ) could be a uniform distribution between 0 and 1.
Bayes' Theorem: Bayesian analysis uses Bayes' theorem to update the prior distribution with new data to obtain the posterior distribution. The formula is:
$$P(\theta | data) = \frac{P(data | \theta) \cdot P(\theta)}{P(data)}$$
- P(θ | data): Posterior distribution (probability of θ given the data)
- P(data | θ): Likelihood (probability of the data given θ)
- P(θ): Prior distribution (probability of θ)
- P(data): Evidence (probability of the data)
Updating the Prior: When new data is observed, the prior distribution is updated to the posterior distribution using the likelihood of the new data. This updated posterior distribution becomes the new prior if more data is collected in the future.

Types of Prior Distributions: A Detailed Examination

Understanding Different Prior Types

In economic analysis, we typically work with three main types of priors, each serving different purposes and reflecting different levels of existing knowledge:

1. Uninformative Priors

Purpose: Express minimal information about the parameter
Economic Use: When analyzing new markets or unprecedented economic phenomena
Example: Analyzing cryptocurrency market behavior in its early stages

2. Weakly Informative Priors

Purpose: Provide some constraints while remaining relatively flexible
Economic Use: When we have some theoretical guidance but limited empirical evidence
Example: Estimating the impact of new technology on productivity

3. Informative Priors

Purpose: Express strong beliefs based on substantial evidence
Economic Use: When analyzing well-studied economic relationships
Example: Estimating price elasticity in established markets

Visualizing and Understanding Different Prior Types

# funnction to compare all prior types with detailed visualisation
compare_all_priors <- function() {
  x <- seq(0, 1, length.out = 1000)
  
  # calculate densities for each prior
  uninformative <- dbeta(x, 1, 1)
  weakly_informative <- dbeta(x, 2, 2)
  informative <- dbeta(x, 8, 2)
  
  # cmbine into data frame
  plot_data <- data.frame(
    x = rep(x, 3),
    density = c(uninformative, weakly_informative, informative),
    Prior = factor(rep(c("Uninformative (Beta(1,1))", 
                        "Weakly Informative (Beta(2,2))", 
                        "Informative (Beta(8,2))"), 
                      each = length(x)))
  )
  
  # Create comparison plot
  ggplot(plot_data, aes(x = x, y = density, color = Prior)) +
    geom_line(size = 1.2) +
    labs(title = "Comparing Different Types of Prior Distributions",
         subtitle = "Economic Parameter Estimation Using Beta Distributions",
         x = "Parameter Value",
         y = "Density") +
    theme_minimal() +
    theme(legend.position = "bottom",
          plot.title = element_text(hjust = 0.5, size = 14),
          plot.subtitle = element_text(hjust = 0.5, size = 12),
          legend.text = element_text(size = 10)) +
    scale_color_manual(values = c("blue", "forestgreen", "red"))
}

# generate comparison plot
prior_comparison <- compare_all_priors()
prior_comparison

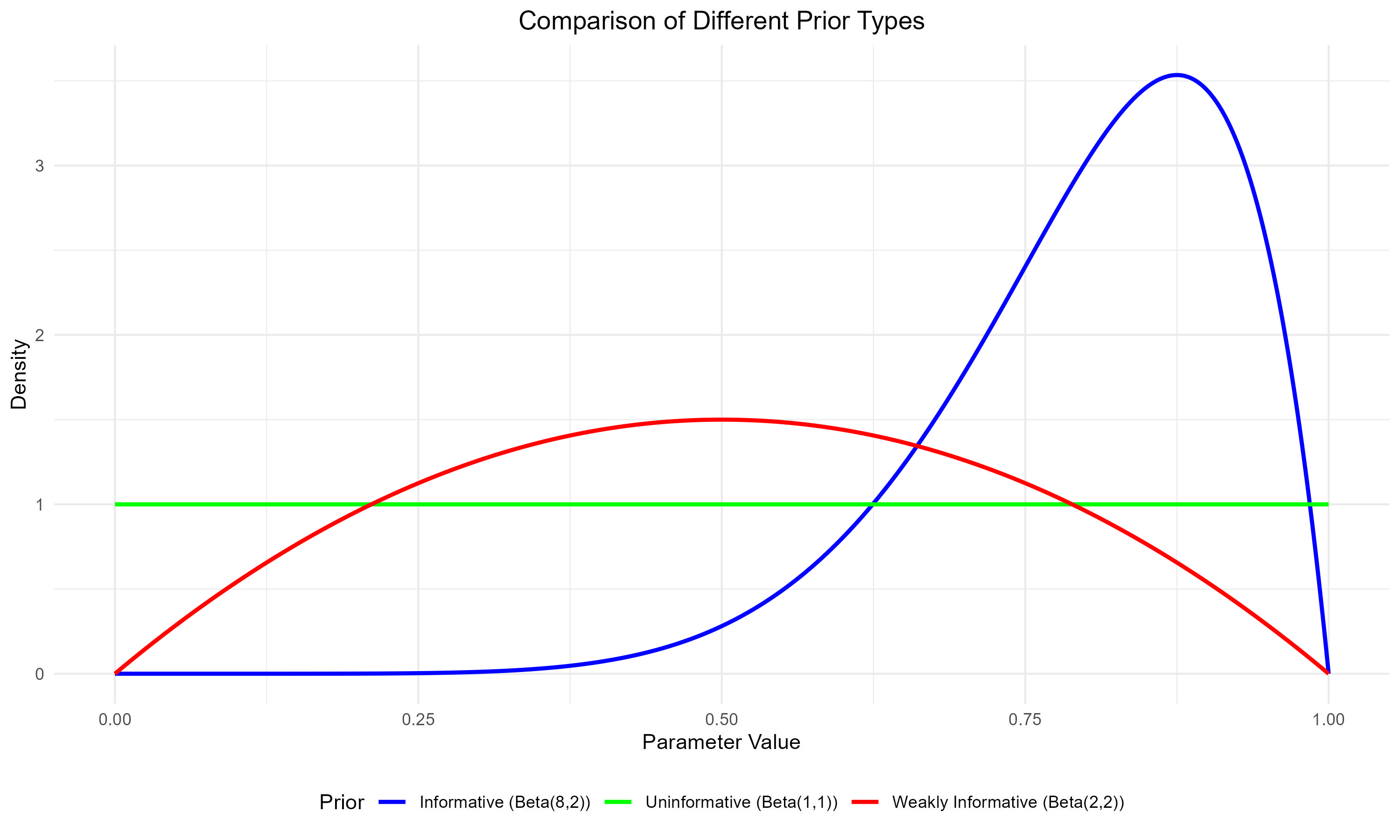
Figure: Comparison of Different Prior Distributions in Economic Analysis

Understanding the Prior Distributions

Green Line: Uninformative Prior (Beta(1,1))

Shape: Completely flat line across all values
Meaning: Equal probability for all possible parameter values
Economic Example: When analyzing a completely new market or economic phenomenon
- Example: Estimating adoption rates for a revolutionary technology
- Use when: No reliable historical data or theoretical guidance exists

Red Line: Weakly Informative Prior (Beta(2,2))

Shape: Gentle hill shape, slightly favoring middle values
Meaning: Mild preference for moderate values while still allowing for extremes
Economic Example: Estimating price elasticity in an emerging market
- Example: New product category with some similarities to existing markets
- Use when: You have general economic theories but limited specific data

Blue Line: Informative Prior (Beta(8,2))

Shape: Strongly peaked curve, concentrated in a specific region
Meaning: Strong beliefs about likely parameter values
Economic Example: Estimating returns in established markets
- Example: Analyzing price effects in mature consumer goods markets
- Use when: Substantial historical data and robust theoretical understanding exists

Some Additional Information

Data Requirements:
- Uninformative prior: Requires more data to reach precise conclusions
- Informative prior: Can reach meaningful conclusions with less data
Robustness:
- Uninformative prior: More robust to unexpected patterns
- Informative prior: More efficient when assumptions are correct
Application:
- Choose based on confidence in prior knowledge
- Consider sensitivity analysis with different priors for important decisions

Understanding Priors (Some Examples): The Market Intuition

Think of Bayesian priors like market expectations. Just as stock prices reflect all currently available information before new earnings announcements, priors represent our collective knowledge before seeing new data.

Market Analogy

Imagine you're investing in a company:

Prior Knowledge (Your Prior): Historical performance, industry trends, management quality
New Information (Data): Quarterly earnings report
Updated View (Posterior): Your revised investment decision

This is exactly how Bayesian analysis works in economics!

Why Priors Matter in Economic Decision Making

Real-World Applications

Central Bank Policy
- Prior belief: Relationship between interest rates and inflation
- New data: Monthly economic indicators
- Decision: Interest rate adjustments
Market Analysis
- Prior belief: Seasonal patterns in consumer spending
- New data: Current sales figures
- Decision: Inventory management
Policy Impact Assessment
- Prior belief: Effect of minimum wage on employment
- New data: Regional employment statistics
- Decision: Policy recommendations

Bayesian vs. Frequentist: A Practical Comparison

Aspect	Frequentist Approach	Bayesian Approach	Economic Implication
Uncertainty	Fixed parameters, random data	Random parameters, fixed data	Better reflects market uncertainty
Small Samples	Often unreliable	Can leverage prior knowledge	Useful for rare economic events
Updating	Requires complete reanalysis	Sequential updating possible	Ideal for real-time economic monitoring
Interpretation	p-values, confidence intervals	Direct probability statements	More intuitive for policy makers

The Power of Priors: Economic Advantages

Why Economists Love Bayesian Methods

Handling Limited Data
Many economic questions have limited data (think major policy changes or financial crises). Bayesian methods let us combine sparse data with economic theory.
Real-Time Decision Making
Central banks can't wait for decades of data to make decisions. Priors help make informed choices with incomplete information.
Model Uncertainty
Economics often has competing theories. Bayesian methods let us weight different models and combine their insights.

Case Study 1: GDP Growth Rate Analysis

Understanding Growth Rate Expectations

When analyzing GDP growth rates, economists consider different scenarios based on varying levels of economic optimism and uncertainty:

1. Conservative Growth Scenario

Expectation: Moderate, stable growth around 2%
Uncertainty: Low - high confidence in estimate
Economic Context: Mature economies in stable periods

2. Optimistic Growth Scenario

Expectation: Higher growth around 3.5%
Uncertainty: Moderate
Economic Context: Emerging markets or recovery periods

3. Uncertain Growth Scenario

Expectation: Moderate growth but highly uncertain
Uncertainty: High - wide range of possible outcomes
Economic Context: Periods of structural change or crisis

# function to compare different GDP growth scenarios
compare_growth_scenarios <- function() {
  x <- seq(-0.05, 0.10, length.out = 1000)  # Range from -5% to 10% growth
  
  # calculate densities for different scenarios
  conservative <- dnorm(x, mean = 0.02, sd = 0.01)
  optimistic <- dnorm(x, mean = 0.035, sd = 0.015)
  uncertain <- dnorm(x, mean = 0.02, sd = 0.03)
  
  # Combine into data frame
  plot_data <- data.frame(
    x = rep(x, 3),
    density = c(conservative, optimistic, uncertain),
    Scenario = factor(rep(c("Conservative (μ=2%, σ=1%)", 
                        "Optimistic (μ=3.5%, σ=1.5%)", 
                        "Uncertain (μ=2%, σ=3%)"), 
                      each = length(x)))
  )
  
  # Crreate comparison plot
  ggplot(plot_data, aes(x = x, y = density, color = Scenario)) +
    geom_line(size = 1.2) +
    labs(title = "Different Scenarios for GDP Growth Rate Expectations",
         subtitle = "Comparing Various Growth Outlooks",
         x = "GDP Growth Rate",
         y = "Density") +
    theme_minimal() +
    theme(legend.position = "bottom",
          plot.title = element_text(hjust = 0.5, size = 14),
          plot.subtitle = element_text(hjust = 0.5, size = 12),
          legend.text = element_text(size = 10)) +
    scale_x_continuous(labels = scales::percent) +
    scale_color_manual(values = c("blue", "forestgreen", "red"))
}

# Generate comparison plot
growth_scenarios_comparison <- compare_growth_scenarios()
growth_scenarios_comparison

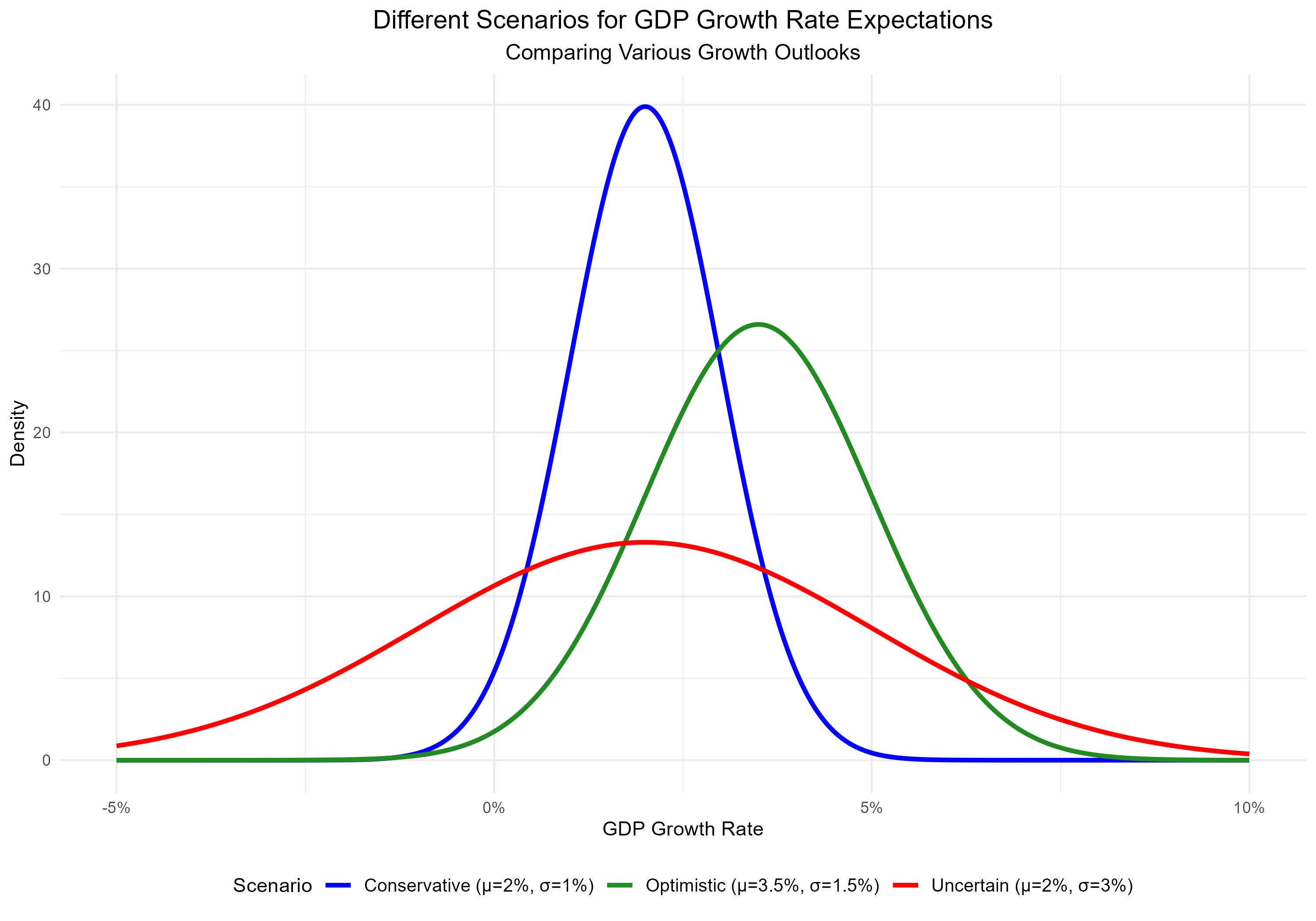
Figure: Comparison of Different GDP Growth Rate Scenarios

Understanding the Growth Scenarios

Blue Line: Conservative Growth Scenario

Shape: Narrow, peaked distribution centered at 2%
Interpretation: High confidence in moderate growth
Economic Context:
- Typical for developed economies in stable periods
- Based on well-established historical patterns
- Limited deviation expected from the mean

Green Line: Optimistic Growth Scenario

Shape: Slightly wider distribution centered at 3.5%
Interpretation: Expectation of higher growth with moderate uncertainty
Economic Context:
- Common in emerging markets or recovery phases
- Incorporates positive structural changes
- Allows for more variation in outcomes

Red Line: Uncertain Growth Scenario

Shape: Wide, flattened distribution centered at 2%
Interpretation: High uncertainty about growth prospects
Economic Context:
- Typical during major economic transitions
- Reflects structural uncertainties
- Accommodates wide range of possible outcomes

Case Study 2: Monetary Policy Effects

Understanding Monetary Policy Transmission

When analyzing how interest rates affect inflation, central banks consider different scenarios about policy effectiveness:

1. Strong Policy Effect

Expectation: Significant negative impact on inflation
Magnitude: Large response to rate changes
Context: Well-functioning monetary transmission mechanisms

2. Moderate Policy Effect

Expectation: Moderate impact on inflation
Magnitude: Standard policy effectiveness
Context: Normal economic conditions

3. Weak Policy Effect

Expectation: Limited impact on inflation
Magnitude: Reduced policy effectiveness
Context: Structural impediments or near zero-lower bound

# Function to compare different monetary policy effects
compare_policy_effects <- function() {
  x <- seq(-1.5, 0.5, length.out = 1000)
  
  # Calculate densities for different scenarios
  strong_effect <- dnorm(x, mean = -0.5, sd = 0.15)
  moderate_effect <- dnorm(x, mean = -0.3, sd = 0.2)
  weak_effect <- dnorm(x, mean = -0.1, sd = 0.1)
  
  # Combine into data frame
  plot_data <- data.frame(
    x = rep(x, 3),
    density = c(strong_effect, moderate_effect, weak_effect),
    Effect = factor(rep(c("Strong Effect (μ=-0.5, σ=0.15)", 
                         "Moderate Effect (μ=-0.3, σ=0.2)", 
                         "Weak Effect (μ=-0.1, σ=0.1)"), 
                      each = length(x)))
  )
  
  # Create comparison plot
  ggplot(plot_data, aes(x = x, y = density, color = Effect)) +
    geom_line(size = 1.2) +
    geom_vline(xintercept = 0, linetype = "dashed", color = "gray") +
    labs(title = "Different Scenarios of Monetary Policy Effectiveness",
         subtitle = "Impact of Interest Rates on Inflation",
         x = "Policy Effect Coefficient",
         y = "Density") +
    theme_minimal() +
    theme(legend.position = "bottom",
          plot.title = element_text(hjust = 0.5, size = 14),
          plot.subtitle = element_text(hjust = 0.5, size = 12),
          legend.text = element_text(size = 10)) +
    scale_color_manual(values = c("blue", "forestgreen", "red"))
}

# Generate comparison plot
policy_effects_comparison <- compare_policy_effects()
policy_effects_comparison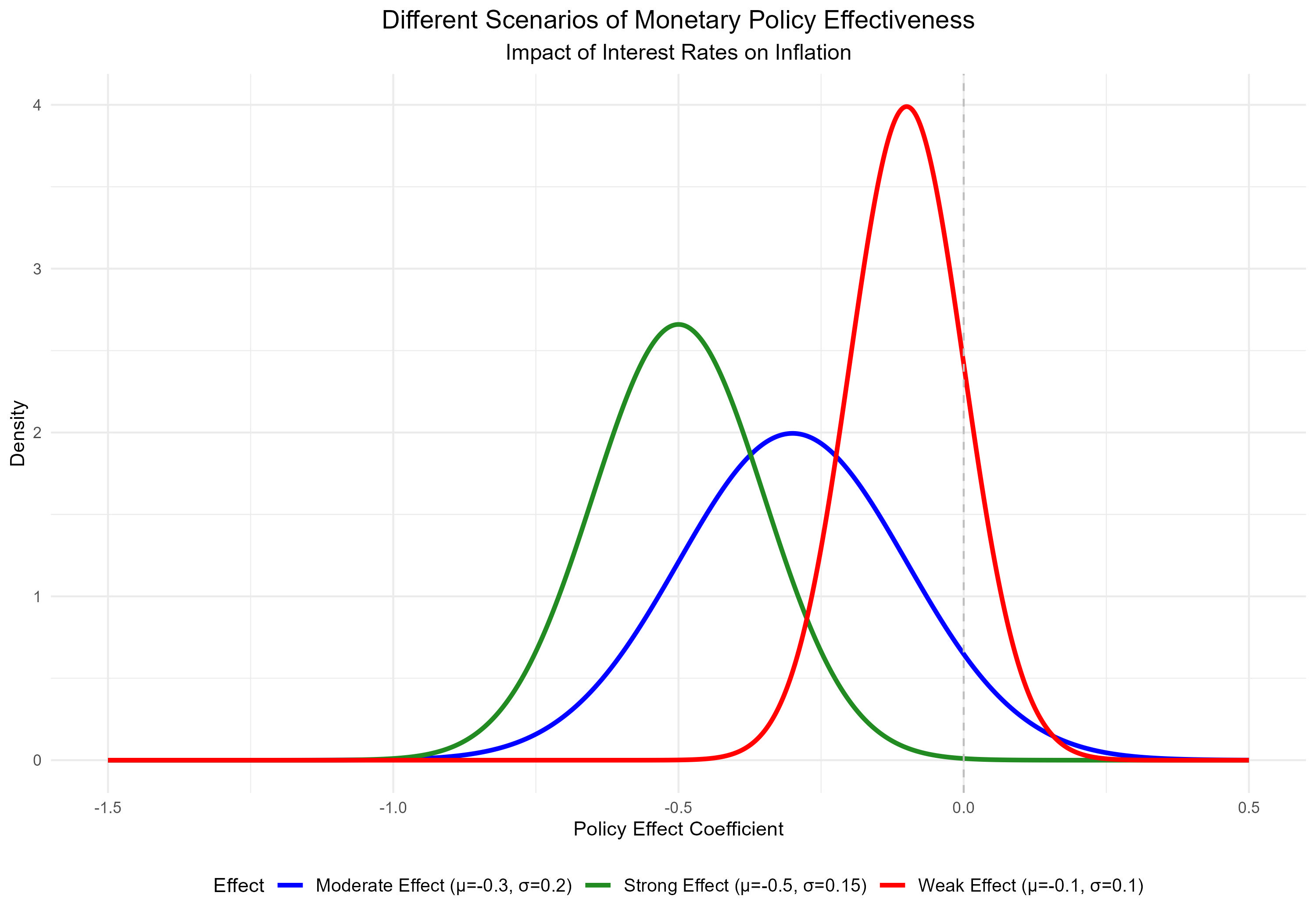

Figure: Comparison of Different Monetary Policy Effect Scenarios

Understanding the Monetary Policy Scenarios

Green Line: Strong Policy Effect

Shape: Sharp peak far from zero, relatively narrow spread
Interpretation: High confidence in strong policy transmission
Economic Context:
- Well-functioning financial markets
- High credit channel effectiveness
- Strong central bank credibility

Blue Line: Moderate Policy Effect

Shape: Broader distribution with moderate negative mean
Interpretation: Standard policy effectiveness with some uncertainty
Economic Context:
- Normal economic conditions
- Typical transmission mechanisms
- Average market responsiveness

Red Line: Weak Policy Effect

Shape: Peak closer to zero, narrow spread
Interpretation: Limited policy effectiveness
Economic Context:
- Near zero lower bound
- Impaired transmission mechanisms
- Structural economic challenges

Conclusion

Bayesian methods offer economists powerful tools for incorporating prior knowledge, handling uncertainty, and making decisions with limited data. The ability to update beliefs systematically as new information arrives makes these methods particularly valuable for policy analysis and economic forecasting.

Key Takeaways

Priors provide a formal way to incorporate economic theory and expert knowledge
Bayesian updating allows for dynamic decision-making in economic policy
Hierarchical models help analyze complex economic structures
Sensitivity analysis ensures robust economic conclusions